optimizeConfiguredParameters ( closure costFunction , boolean _maximize , boolean _fastButLessAccurate , boolean _verboseReturn , map _hyperparameters , string _idOptimSystem ) : mixed
This function proposes to use two AI algorithms to optimize the value of the optimized parameters specified in the script.
The general approach
1) You build an expert system analyzing data by establishing subjective rules built with your expertise. It is recommended to build a deterministic expert system (same input, same output) so that the cost function can have a zero differential.2) You replace the subjective coefficients of these rules by optimized parameters
3) You optimize these parameters when running in learning mode, this will take a little more time. This optimization is done thanks to a cost function symbolizing the penalties (or the good scores) collected with a certain configuration of the optimized parameters. It is preferable to calculate this cost function on a large number of data of course.
4) Multiple values will be tested. The algorithm is intelligent and will favor promising directions in order to minimize the number of tests to do and the number of evaluation of the cost function which can be expensive. At each iteration, the value returned by optimizedParameter will change according to what the algorithm wants to test
5) At the end of the process, when the maximum number of iterations is exceeded or when the value of the cost function does not evolve much, the process is exited and the optimized parameters are saved in a configuration considered as optimal.
6) The next use of optimizedParameter will use these optimized values, so you don't have to do the learning process each time ( happily !)
Note: you can reset the optimized system deleting the file OPTIM_variables_
Note 2: if initial values are not used in optimizedParameter, the first point will have all these coordinates at 1 : vector(1, 1, 1, 1, ...unil the last dimension)
Example of a cost function:
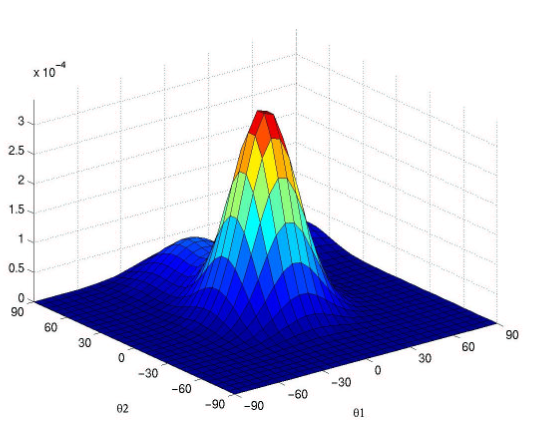
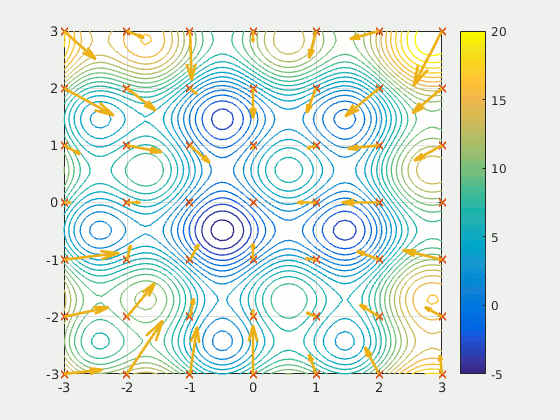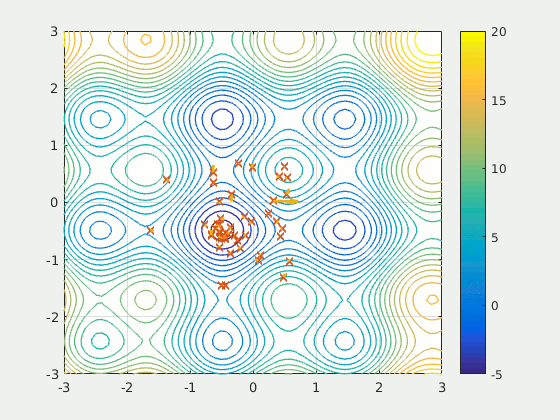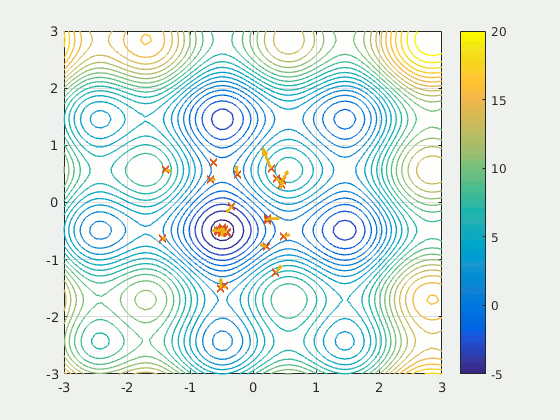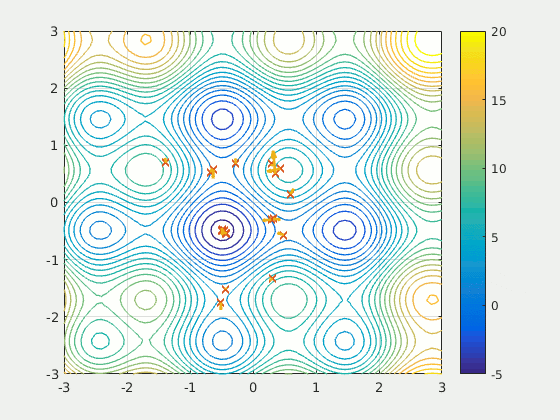
Problems related to the optimization
This function proposes numerical methods of non-linear analysis that do a heuristic analysis, in other words the mathematical problem is not solved in a formal way (with derivatives).Artificial intelligence can be wrong. Like any human being it introduces the possibility of stupidity. You should not consider this function as a magic tool to be used quickly without any work on your part. It will accompany your engineering work, not replace it.
Two concerns are common:
- The limits are reached and the function degenerates. In other words, it only uses values close to the bounds and constantly returns to them, causing cascading problems on the other variables
- The algorithm ends up trapped in a local minimum and does not reach the global minimum. Imagine that you are in a well with steep slopes and that you want to reach the next deeper well but you can't get up from the first one. The algorithm is a victim of this phenomenon because it is confident and has reduced the step too much.
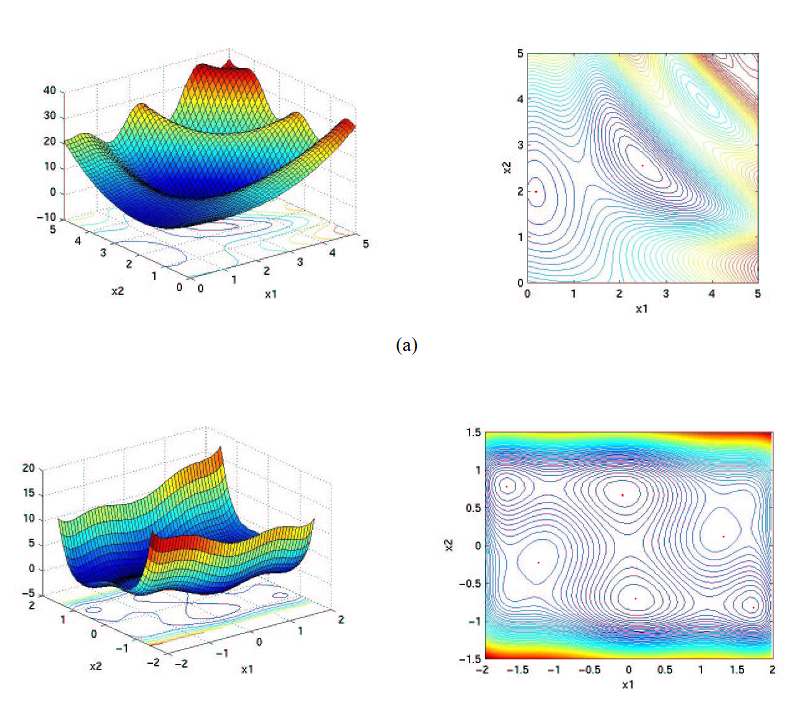
To avoid these problems, it is necessary to adapt the hyper-parameters of the algorithms and to play on the steps and the initial values of the optimized arguments in order to get out of these situations. A conservative and measured configuration can be reached after several tries. Display the results of the iterations to get an idea of their evolution or save them in a CSV to produce graphs translating their evolution.
Example
A purely mathematical illustration of an optimization problem with a learning mode and without learning mode:withTraining = true //training can take time, often we will do it at selected times. If this variable is set to false, the script will be launched with the last optimized parameters, when the script was launched with learning
//function to optimize (it is a difficult function with a lot of local minimums)
costFunction = {x=null, y=null ->
if(equals(x, null) && equals(y, null)) //if y and x are not null, they are manually indicated - it is for us, we want to play this this function
{
//parameters with configuration - this is used by the optimizer, because x and y are not indicated in optimizeConfiguredParameters
x = optimizedParameter("x", -10, 10, 5)
y = optimizedParameter("y", -10, 10, 5)
}
//calculate the cost
cost = (x == 0 || y == 0) ? 0 : Math.atan(x) * Math.atan(x + 2) * Math.atan(y) * Math.atan(y) / (x * y)
//display each iteration the result
console("iteration ("+x+", "+y+") = "+cost)
return cost
}
console("TESTS")
//some values
costFunction(2,1) // = 0.45
costFunction(20,10) // = 0.02
costFunction(-3,1) // = -0.20
costFunction(0,0) // = 0
//and a minimum
costFunction(0.23,-1.39) // = -0.729
if(withTraining)
{
//initial call to instantiate configurations of optimizedParameter (we need it to run correctly optimizeConfiguredParameters), initial values will be used
costFunction()
//let's optimize!
console(optimizeConfiguredParameters(costFunction, false)) //{optimumValue=-0.7290400707055188, optimumCoordinates={x=0.22866822487692323, y=-1.3917452051913402}, nbEvaluations=48}
}
console("Best parameters are "+optimizedParameter("x")+", "+optimizedParameter("y")+
". Final point is "+costFunction(optimizedParameter("x"), optimizedParameter("y"))+
" (same than "+costFunction()+")"
)In this more realistic example, we will imagine a system to evaluate if a document is an ID card by creating our own rules and optimizing them:
listTrueIdCards = ["id_card1.jpg", "id_card2.jpg"] //The expert filled in this table himself, he made a visual check on each document and evaluated which ones were really identity cards
costFunction = {returnIdCard = false->
totalCost = 0
idCards=[]
for(document in listFiles(path("desktop")+"documents/"))
{
text = ocr(path("desktop")+"documents/"+document, "C:\\Program Files\\ImageMagick-7.1.0-Q16-HDRI\\magick.exe") //we extract the text of the document
nbInterstingTerms = count(regexAll(/(?si)((ID card)|(United States)|(official))/, text)) //This indicator gives an idea of the semiotic relevance of the document content
nbCaracters = count(text) //This indicator is more coarse, basically if there are a lot of characters we are on a page of novel and if there are few on an official document
factorInterstingTerms = optimizedParameter("factorInterstingTerms", 4, 7, 6, 2) //We trust this parameter, we will try to give it a high coefficient, even if we leave it to the optimizer to criticize it
factorNbCaracters = optimizedParameter("factorNbCaracters", 0, 4, 1, 2) //We give the possibility to cancel the coefficient if this parameter is useless, but it can theoretically have the same weight of 4 as the other, it is the choice of the expert
//This score and its parameters are the core of this small expert system. We translate human reasoning into rules (expert system), while mixing it with AI (optimization)
scoreDocument = factorInterstingTerms * nbInterstingTerms + factorNbCaracters * nbCaracters
isIdCardInReality = arrayContains(listTrueIdCards, document) //Is the document actually an identity card? We will use it to evaluate if the expert system is right or wrong
if(scoreDocument > optimizedParameter("scoreLimit", 1, 15, 8, 5)) //Above a certain score the document is considered validated. We start with a limit of 8
{ //the AI says it is an ID card
if(isIdCardInReality) totalCost += 1 //The AI is right, we add a reward to the total evaluated by the optimizer
else totalCost -= 1 //We made a mistake, we add a penalty instead
if(returnIdCard) idCards.add(document) //In case you are not learning
}
else
{ //the AI says it is NOT an ID card
if(isIdCardInReallty) totalCost -= 1 //false-negative -> penalty
else totalCost += 1 //true negative -> reward
}
}
//Depending on if we are training or not we return either the score of the cost function or we transform the cost function into a business function and we extract the list of identity cards
return returnIdCard ? idCards : totalCost
}
//training
optimizeConfiguredParameters(costFunction, true)
//display all ID cards found by the optimized expert system
console(costFunction(true))Instead of creating two modes inside the script, one for normal operation and another for training, we can manage a normal operation script and optimize its parameters by importing it into a second script. You just have to calculate the score of the cost function in the first script to be able to retrieve it (or you can put a calculateScore variable just before the importScript to activate this calculation because it will be retrieved in the imported script if it exists)
costFunction = {->
importScript(105723) //this script contains optimizedParameters using the ID "myOptimSystemID" and a score variable which is retrieved after the importScript (because all variables are accessed with an importScript)
return score
}
optimizeConfiguredParameters(costFunction, true, false, false, null "myOptimSystemID") //Be careful to use the same ID as in the optimizedParametersSee also
optimizedParameterParameters
costFunction
Cost function to be optimized. Its value indicates whether or not the parametric optimization is going in the right direction. It is more efficient if it combines the results of a large number of data (but then it takes more time to be computed).
It is a Grimport closure and is called without parameters. So if you use it, remember to provide default values so that the cost function remains accessible. The function must contain all optimized parameters called with optimizedParameter. It must always return a number.
It is a Grimport closure and is called without parameters. So if you use it, remember to provide default values so that the cost function remains accessible. The function must contain all optimized parameters called with optimizedParameter. It must always return a number.
_maximize (optional)
By default at true, the algorithm try to maximizate the value of the cost function. Else it is minimized.
_fastButLessAccurate (optional)
Default:true. Conditions the choice of the algorithm used:
- _fastButLessAccurate = true. This is a very good algorithm. It will scan the area much faster than the second algorithm but this is at the expense of accuracy (exploration/exploitation trade-off). It has the defect of often ignoring the initial position to start at the boundaries if the space between the boundaries is insufficient for the construction of the first quadratic model. It is less complex to parameterize and allows to be sparing on the use of the cost function. It is particularly well adapted to high dimensional problems. In most cases, it outperforms the Powell optimizer significantly.
- _fastButLessAccurate = false. Succeeds more often and is based on stochastic algorithms, but is more expensive to run. It is an implementation of the active evolution strategy of covariance matrix adaptation. It is a reliable stochastic optimization method that should be applied if derivative-based methods, e.g. quasi-Newton BFGS or conjugate gradient, fail due to a rough search landscape (e.g. noise, local optima, outlier, etc.) of the cost function. It does not estimate or use gradients, which makes it much more reliable in terms of finding a good solution, or even the optimal one. It is particularly well suited to non-separable and/or ill-conditioned problems.
- _fastButLessAccurate = true. This is a very good algorithm. It will scan the area much faster than the second algorithm but this is at the expense of accuracy (exploration/exploitation trade-off). It has the defect of often ignoring the initial position to start at the boundaries if the space between the boundaries is insufficient for the construction of the first quadratic model. It is less complex to parameterize and allows to be sparing on the use of the cost function. It is particularly well adapted to high dimensional problems. In most cases, it outperforms the Powell optimizer significantly.
- _fastButLessAccurate = false. Succeeds more often and is based on stochastic algorithms, but is more expensive to run. It is an implementation of the active evolution strategy of covariance matrix adaptation. It is a reliable stochastic optimization method that should be applied if derivative-based methods, e.g. quasi-Newton BFGS or conjugate gradient, fail due to a rough search landscape (e.g. noise, local optima, outlier, etc.) of the cost function. It does not estimate or use gradients, which makes it much more reliable in terms of finding a good solution, or even the optimal one. It is particularly well suited to non-separable and/or ill-conditioned problems.
_verboseReturn (optional)
Default: true, returns the number of evaluation, the optimized parameters and the optimized value of the cost function.
If false, it returns the optimized parameters
If false, it returns the optimized parameters
_hyperparameters (optional)
An associative array containing all general parameters of the AI optimizer. Ex :["defaultStandardDeviation":2.5, "maxEvaluations":500]
• "maxEvaluations" (default:100) : Maximum number of evaluations of the cost function
• "initialWithLastOptimizedValues" (default:false) : Allows to initialize the optimizer with the values of the last optimization rather than the one in the initial argument of optimizedParameter. You start at a position closer to an extremum but to encourage exploration, think of playing with the steps
• "saveParametersEachIteration" (default:true) : Save the settings at each iteration. Allows you to stop the algorithm while it is optimizing and still keep the results when you notice that it is not moving much. Otherwise the optimized parameters are only saved at the very end of the optimizer and you will lose them if you interrupt the process.
• "defaultStandardDeviation" (default:1) : If you did not specify the initialstep argument in optimizedParameter, this value is used instead.
• "numIterpolationPoints" (default:(dimension+1)*(dimension+2)/2 ) just if _fastButLessAccurate = true : Number of interpolation conditions. For a problem of dimension {n}, its value must be in the interval {[n+2, (n+1)(n+2)/2]}. Choices that exceed {2n+1} are not recommended.
• "lambda" (default:4 + 3 * ln(dimension) ) just if _fastButLessAccurate = false : Population size, offspring number. The primary strategy parameter to play with, which can be increased from its default value. Increasing the population size improves global search properties in exchange to speed. Speed decreases, as a rule, at most linearly with increasing population size. It is advisable to begin with the default small population size.
• "maxIterations" (default:30000) just if _fastButLessAccurate = false : Maximal number of iterations in the algotihm
• "stopAfterCostValue" (default:none) just if _fastButLessAccurate = false : Whether to stop if objective function value is smaller than this value
• "isActiveCMA" (default:true) just if _fastButLessAccurate = false : Chooses the covariance matrix update method.
• "checkFeasableCount" (default:0) just if _fastButLessAccurate = false : Determines how often new random objective variables are generated in case they are out of bounds.
• "maxEvaluations" (default:100) : Maximum number of evaluations of the cost function
• "initialWithLastOptimizedValues" (default:false) : Allows to initialize the optimizer with the values of the last optimization rather than the one in the initial argument of optimizedParameter. You start at a position closer to an extremum but to encourage exploration, think of playing with the steps
• "saveParametersEachIteration" (default:true) : Save the settings at each iteration. Allows you to stop the algorithm while it is optimizing and still keep the results when you notice that it is not moving much. Otherwise the optimized parameters are only saved at the very end of the optimizer and you will lose them if you interrupt the process.
• "defaultStandardDeviation" (default:1) : If you did not specify the initialstep argument in optimizedParameter, this value is used instead.
• "numIterpolationPoints" (default:(dimension+1)*(dimension+2)/2 ) just if _fastButLessAccurate = true : Number of interpolation conditions. For a problem of dimension {n}, its value must be in the interval {[n+2, (n+1)(n+2)/2]}. Choices that exceed {2n+1} are not recommended.
• "lambda" (default:4 + 3 * ln(dimension) ) just if _fastButLessAccurate = false : Population size, offspring number. The primary strategy parameter to play with, which can be increased from its default value. Increasing the population size improves global search properties in exchange to speed. Speed decreases, as a rule, at most linearly with increasing population size. It is advisable to begin with the default small population size.
• "maxIterations" (default:30000) just if _fastButLessAccurate = false : Maximal number of iterations in the algotihm
• "stopAfterCostValue" (default:none) just if _fastButLessAccurate = false : Whether to stop if objective function value is smaller than this value
• "isActiveCMA" (default:true) just if _fastButLessAccurate = false : Chooses the covariance matrix update method.
• "checkFeasableCount" (default:0) just if _fastButLessAccurate = false : Determines how often new random objective variables are generated in case they are out of bounds.
_idOptimSystem (optional)
You can give an ID to your optimized parameter set. If you don't specify anything, the unique id of the script will be used. This parameter is especially useful if you mix several optimizers in one script or if you copy and paste them.
